Released January 2017
Introduction
This white paper is a part of Wilary Winn’s series of white papers regarding the Current Expected Credit Loss (CECL) Model and highlights best practices in collecting data for CECL. Our prior white papers include:
• Implementing the Current Expected Credit Loss (CECL) Model – November 2016
• Making the Business Case for CECL Part I – ALM and Capital Stress Testing – December 2016
• Making the Business Case for CECL Part II – Concentration Risk – February 2017
Wilary Winn believes that the information financial institutions should collect as they work to implement CECL is primarily dependent on:
• The type of loans being assessed; and
• The credit risk model the financial institution plans to use.
Data Collection for CECL
As mentioned above, Wilary Winn believes that the information a financial institution should collect while working to implement CECL is mainly dependent on the type of loans being assessed and the credit risk model the institution plans to use. We also believe these factors are interdependent. For example, we believe loss estimates for commercial real estate (CRE) loans should be based on a full credit analysis on loans with the highest levels of credit risk (high risk ratings) and a migration analysis for CRE loans with low levels of credit risk (low risk ratings). Conversely, we believe loss estimates for relatively homogenous loans such as residential real estate and consumer loans are best modeled using statistical techniques.
The CECL standard requires expected losses to be measured on a pooled basis whenever similar risk characteristics exist. The standard permits the cohort pool to be developed based on a long list of characteristics including year of origination, financial asset type, size, term, geographical location, etc.[1]
Wilary Winn believes the cohorts from which loss assumptions will be derived should be based on comparative credit performance and on the loan cohort’s sensitivity to predictive credit inputs.
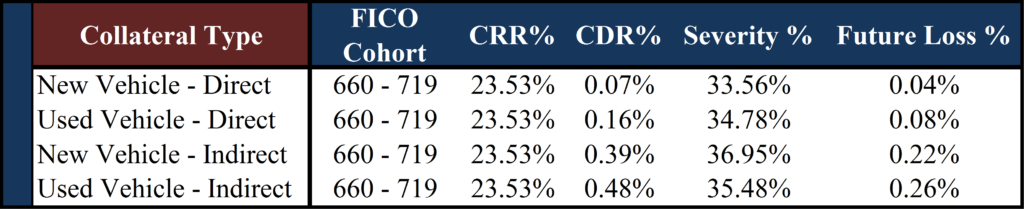
For example, we believe vehicle loans should be first grouped into four major categories because of the differing expected credit performance even within the same FICO cohort – differentiating between new and used and direct versus indirect. The table below shows the importance of choosing sub-categories as the new vehicle direct group performs 6 ½ times better than the used indirect category within the same FICO cohort.
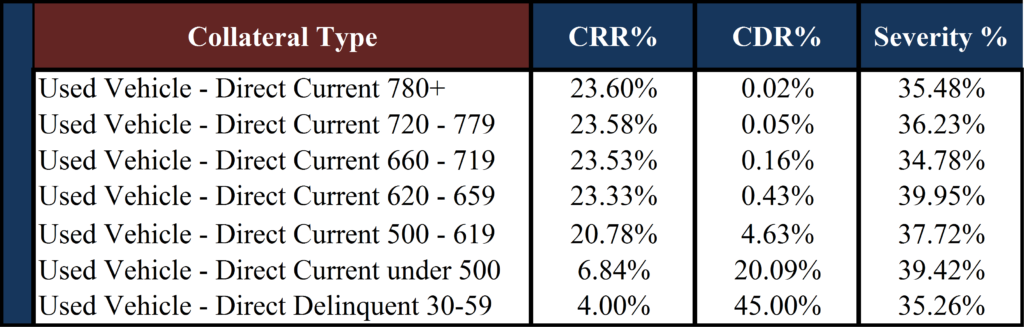
After establishing the initial product division criteria for a homogenous loan type, we then believe these categories should be further divided into FICO bands as historical credit losses have varied significantly by credit score range. The table below segments the used vehicle direct category by credit score and shows voluntary repayment (conditional repayment rate or CRR), involuntary repayment (conditional default rate or CDR) and estimated loss severity. Not surprisingly, the cohorts reflecting the lowest credit score ranges also reflect the highest levels of estimated defaults.
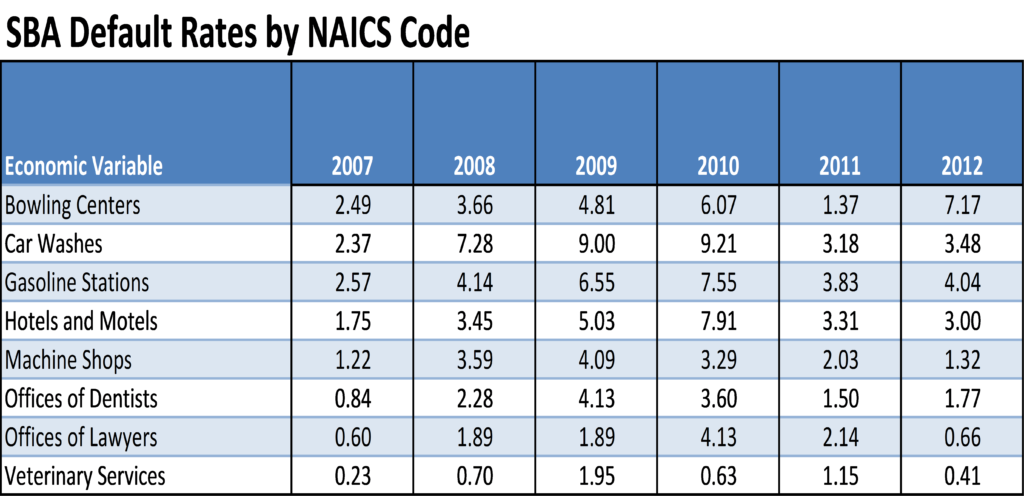
As an example, for business lending we believe that commercial and industrial loans should be segmented by type of business due to historical levels of credit loss variance. The following table shows the default rates reported by the Small Business Administration (SBA) from 2007 to 2012 for certain business types. The collateral classification for the SBA loans is determined with the North American Industry Classification System (NAICS) code. As shown in the following table, in 2012 the default rate for SBA loans to bowling centers was 7.17% whereas the default rate for veterinary services was .41%.
Wilary Winn believes that loan cohorts should be based on a financial institution’s lending strategies and portfolio characteristics and that an institution should expend considerable effort to determine the loan cohorts from which lifetime credit losses will ultimately be derived. For example, Financial Institution A could have an extensive vehicle lending portfolio with varying credit rates originated from multiple sources. It would want to develop pools that appropriately reflect the risks and would likely benefit by forming vehicle loan pools similarly to the process we described above. Conversely, Financial Institution B could have an insignificant vehicle loan portfolio, perhaps even an insignificant consumer loan portfolio. It could base its pool on vehicle loans in total or even consumer loans in total. After an institution has divided its loan portfolio into cohorts, it then needs to select the model it will use to estimate expected credit losses. FASB and the banking regulators have made it very clear that financial institutions can select the methodology that best suits their needs. The most common models include loss estimates based on:
- Average charge-off method – the historic averages for similar loan pools (e.g., new vehicle loss rates have averaged x%)
- Static pool – on loan pools with similar risk characteristics originated within a similar period of time (e.g., used indirect vehicle loans with FICOs from 720 to 780 originated within the most recent 5 years).
- Vintage analysis – the age of the loan and would generally include loss curves (e.g., the loss rate for a pool was .x% in year one and .y% by year two)
- Migration or roll-rate analyses – the likelihood of a loan moving to default (e.g., using historical trends in risk rate changes to infer probable future losses)
- Discounted cash flow – the loan’s contractual cash flows are adjusted for estimated prepayments, defaults and loss severity and then discounted back to the origination date at the note rate
Continuing with our vehicle loan example, let us assume that a financial institution elects to estimate lifetime credit losses based on a vintage analysis. The example below shows the actual cumulative losses by month since origination for a financial institution’s new vehicle direct portfolio with a 24-month original term. The concept with estimating credit losses using vintage analysis is to infer the future loss rates by comparing performance-to-date for an origination year to historic rates of default when the past pool was of similar age. For example, one way to estimate the loss rate to be incurred of the Quarter Two 2014 vintage in its final quarter of life is take the 1.23% incurred for the quarter ending at 21 months and add the average increase of .27% that historically occurred between 21 months and 24 months (3.44% – 3.17%). As shown in the following table, the result is an estimated cumulative loss rate for the final quarter of the Quarter Two 2014 vintage of 1.50%.
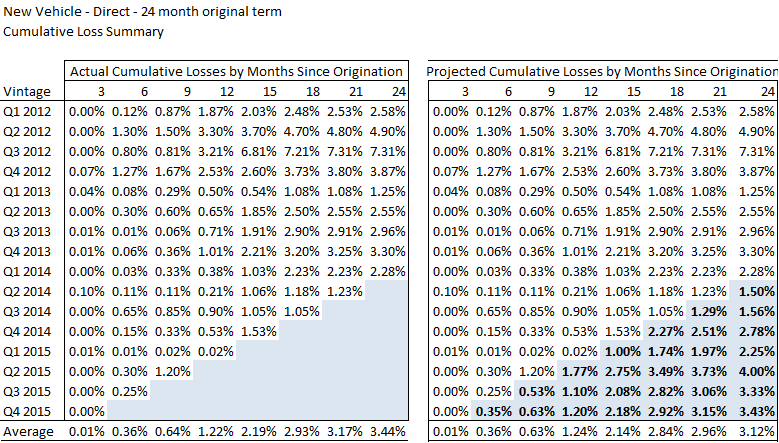
To implement a vintage analysis a financial institution needs to identify the total amount of loans originated by vintage. This total does not change and is the denominator in the loss rate calculation. We note that our example is highly simplified. We have selected a short initial loan term for ease of presentation. We have also selected a relatively broad loan pool – new vehicle direct regardless of credit grade. To fully implement this methodology a financial institution would need to accumulate loss history by year for each cohort. We strongly recommend that the loss analysis includes a full economic business cycle otherwise the institution will not have sufficient input if and when it faces another economic downturn. In other words, going back only five years when building a static pool analysis will truncate the 2008 through 2010 performance – the most recent trough in the economic cycle and an institution will therefore not have the performance statistics it needs if economic conditions are forecast to downturn similarly. In addition, we recommend that a financial institution electing to use this kind of analysis calculate the weighted average FICO score for each cohort to ensure the credit characteristics are similar or to provide information that can be used to adjust the loss rates in the event they differ.
As a firm, we have elected not to use average charge-off, static pool or vintage analyses to estimate lifetime credit losses for the following reasons:
- The CECL standard requires expected prepayments to be included in the estimate, adding a layer of complexity not captured with these methods – this is particularly true for residential real estate loans;
- It is very difficult to adjust these types of analyses based on only historical performance for changes in underwriting standards; and
- The CECL standard requires that the loss rate adjustments be based on current and forecasted macroeconomic conditions and the historic loss rates were likely calculated based on economic environments that are potentially quite dissimilar.
We think a superior solution is to use discounted cash flow (DCF) models that are based on updated credit inputs. WW Risk Management believes that by first establishing detailed loan cohorts, successfully obtaining updated predictive credit attributes, and performing a discounted cash flow analysis will lead to the most precise calculation possible of lifetime credit losses.
As a reminder, discounted cash flow methods begin with the loan portfolio’s contractual cash flows, which are the adjusted using three input assumptions:
- Conditional repayment rate (CRR) the annual percentage rate of voluntary prepayments
- Conditional default rate (CDR) – the annual percentage rate of involuntary prepayments – defaults
- Loss severity – the loss to be incurred when a loan defaults
CRR is dependent on the loan’s interest rate compared to existing and forecasted market interest rates – does the borrower have an incentive to refinance the loan and to the loan and credit attributes – does the borrower have the ability to refinance the loan based on its existing loan-to-value ratio and the borrower’s FICO score.
CDR is dependent on the borrowers existing and forecasted FICO score and the existing and forecasted loan-to-value ratio. Loss severity is based on the loan-to-value ratio at the time of the default as well as foreclosure and liquidation costs.
Best practices for implementation of CECL compliant DCF models include being able to successfully obtain updated credit information on the loan portfolio, including, but certainly not limited to: FICO for consumer loans, FICO and combined loan-to-value amounts for residential real estate loans, and NAICS code for commercial and industrial loans.
In addition to obtaining current credit attributes, an institution also needs to collect historical performance data. For example, if an institution elected a DCF modeling technique for its residential real estate closed-end second lien portfolio, we believe it would need to retrieve data on the rate of default and the loss incurred on defaults by FICO and combined loan-to-value ratio by quarter over the most recent economic business cycle. A complete list of the loan information needed to be collected to derive DCF model inputs is attached as Appendix A.
Having discussed the data elements and data gathering strategy, we next address the statistical validity of the historical loss data from the cohorts the financial institution elects to form. We demonstrated earlier in this white paper the advantages of dividing vehicle loans into four major components and further sub-dividing them by FICO score because these refinements produce far more accurate predictions.
However, the more granular and, therefore more predictive a financial institution makes a pool, the fewer historical loan defaults it will contain.
Wilary Winn believes few institutions by themselves have sufficient numbers of defaulted loans by major category – used indirect – let alone by sub-category used indirect 620-659 FICO – to be statistically valid. We therefore believe that financial institutions will derive significant benefit by combining their results with industry wide data. In other words, while the CECL standard requires the use of a financial institution’s experience and that the calculation does not require industry wide inputs, we believe implementing such a “bare bones” model would deprive an institution of significant insights regarding credit performance.
To repeat the example from our white paper Implementing CECL regarding required pool size – we address two questions:
- How large must a pool be in order to be statistically valid?
- How do I incorporate my financial institution’s performance?
How large must a pool be in order to be statistically valid?
To help us answer the first question, we turned to Professor Edward W. Frees, the Hickman Larson Chair of Actuarial Science at the University of Wisconsin – Madison. (For the sake of relative simplicity, we will focus on loan defaults only and omit loss given default or loss severity.) The risk of a loan defaulting is binary – it either does or does not default. In order to determine a required sample size a financial institution needs to determine the margin of error that it can tolerate and the amount of confidence it must have in the results. For illustrative purposes, let us assume we can tolerate a sampling error of 3% with a 95% confidence level.
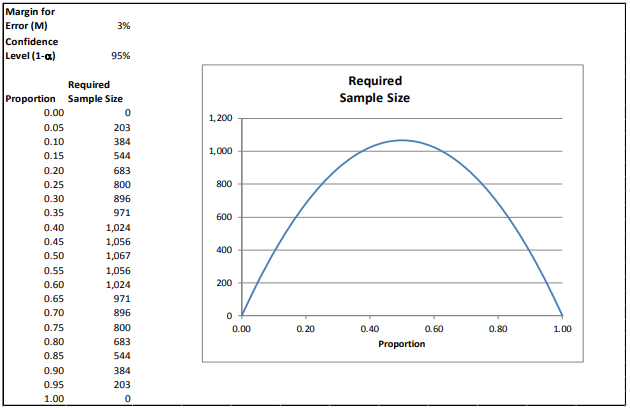
As the reader can see, the required sample sizes are relatively small when the probability of default nears highly certain or highly uncertain (1 or 0, respectively).
We can build on this idea by considering binary risks that are grouped into categories. In this next example, we divide loans into FICO buckets assigning default probabilities from our previous industrywide research – loans with FICOs of 780 and above have a .03% chance of default while loans with FICOs below 500 have a 23.06% chance of default.
In statistical parlance, these differing probabilities of default are called proportions. Because we have differing proportions, we will vary our margins of error in order to derive realistic required sample sizes.
To help us determine the margins of error by FICO band, we turn the idea of financial statement materiality. Let us say we have a financial institution with a $500 million of total assets. For the sake of simplicity, we will assume it has $200 million of fixed rate mortgages and an allowance for loan losses of 0.25% or $500,000. Using a fifteen percent materiality threshold for the allowance we need to produce a loan loss estimate that is reliable to plus or minus $75,000. Let us assume an average loss severity of 23 percent – the rate for FNMA and FHLMC prior to the most recent financial downturn. We can then set our margin of error tolerances based on the dollar amount of loans in each FICO bucket, the number of probable defaults, and the average loss severity.
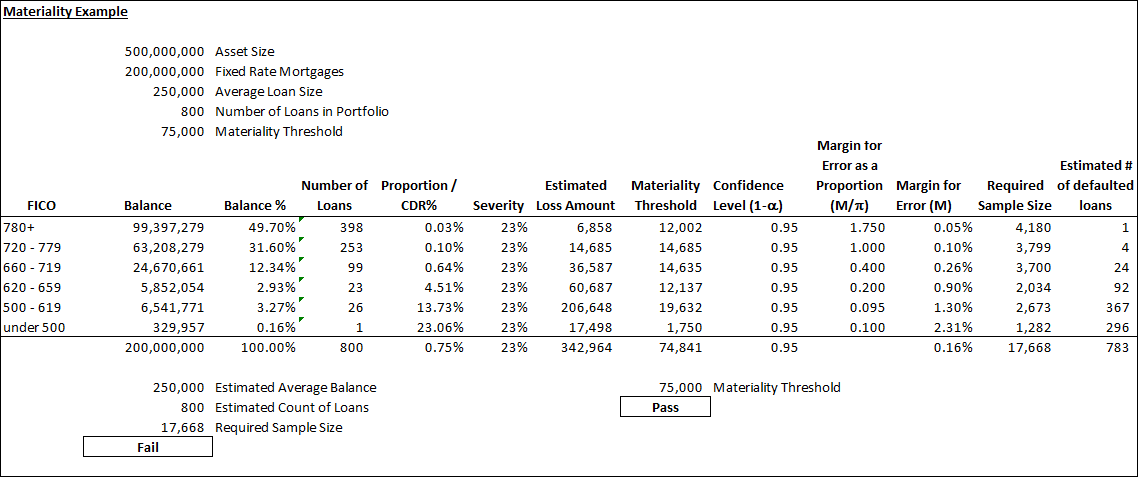
In this case, we can see that the financial institution has an insufficient number of loans in its portfolio to be able to derive a statistically valid result. The required sample size is 17,668 loans in order for our expected credit loss estimate for the portfolio to be within $75,000 and the financial institution has just 800 loans. As a result, it will need to rely on information derived from larger pools. We can also see that our example financial institution does not have sufficient information in the lower risk FICO groupings – the areas with the greatest potential risk. For example, to be statistically accurate a financial institution would need 3,700 loans in the 660-719 group for which we would expect 24 defaults. Our sample financial institution has just 99 loans in this cohort. We believe that this data shortfall for lower quality loans will continue as we continue to move forward into the future from the financial downturn. Nevertheless, we want to incorporate the financial institution’s actual performance into our loss estimates.
This reinforces the need for larger data pools because slicing the groupings again obviously results in fewer loans per predictive indicator.
How do I incorporate my financial institution’s performance?
To help us with the second question of incorporating a financial institution’s actual results, we again turned to Professor Frees and we can learn from another industry. The insurance industry addresses the issue with a concept called “credibility theory”. The idea is to blend a financial institution’s loss rates with industry-wide loss experience. There are many varieties of credibility theory that can be used depending on company expertise and data availability. One variety is “Bayesian credibility theory” that employs statistical Bayesian concepts in order to utilize a company’s understanding of its business and its own experience.
We will use the 500-619 FICO group for our example. Assuming the average loan size for this cohort is also $250,000, we have 26 loans in the group. To estimate our sample size, we used an industry average default rate of 13.73% for the group and our required sample size was 2,673 loans. We assume that 367 of the 2,673 loans in the group will default. To continue our example, let us assume that the financial institution’s actual recent default experience was 49.68% for this FICO cohort. While it first appears that the financial institution’s default probability is worse than the industry average, this could also be due to chance variability. To avoid this potential outcome, we want to incorporate the financial institution’s actual performance into our CDR estimate in a statistically valid way. To do this, we want to be 95% confident that our estimate is within 9.5% of the true default probability, consistent with our required sample size inputs.
Credibility estimators take on the form:
New Estimator = Z × Company Estimator + (1 − Z) × Prior (Industry) Estimator
Although there are many variations of this estimator, most experts express the credibility factor in the form:
Z = n/(n+k)
for some quantity k and company sample size n. The idea is that as the company sample size n becomes larger, the credibility factor becomes closer to 1 and so the company estimator becomes an important in determining the final “new estimator.” In contrast, if the company has only a small sample n, then the credibility factor is close to 0 and the external information is the more relevant determinant of the final “new estimator.”
For our example, using some standard statistical assumptions, one can show that:
k = 4/(L^2 * Prior Estimator)
Here, “L” is the proportion desired (9.5% in our example, margin for error as a proportion or M/π in our prior example notation). Our prior estimate for defaults (“CDR” or proportion) for this band was 13.73%.
To continue, this is k= 4/(L^2 * Prior Estimator) = 4/(9.5^2 * 0.1373) = 3,228. With this, we have the credibility factor Z = 26/(26 + 3,228) = 0.80%
Our final CDR estimate for the 500 to 619 FICO band is equal to our company input (49.68% * 0.80%) + (1 – 0.80%) * 13.73% or 14.02%. We have thus incorporated the financial institution’s performance in this loan category into our CDR estimate in a statistically valid way deriving a lower estimate than had we used the institution’s actual results only.
As clearly demonstrated with the insights obtained from the work of Professor Frees, Wilary Winn believes that industry default data is needed as a supplement to a financial institution’s own internal credit loss experience to establish a CECL process that is accurate with respect to predicting future lifetime losses at the cohort level. This type of loss estimate analysis best lends itself to the discounted cash flow method.
Macroeconomic Inputs
The CECL standard requires that the lifetime loss estimate be based on current and forecasted economic conditions. Regardless of the technique selected, we believe a financial institution should identify the sources it will use for historical analysis and for forecasted changes in macroeconomic conditions. This is more complex than it seems. For example, most would agree that the best source for the historic rates of unemployment is the Bureau of Labor Statistics. However, should an institution collect data at the state level, the county level, the MSA level, etc. We believe this depends on the financial institution’s concentration of loans by geographic area. As another example, should an analysis of changes in housing prices be based on data from the Federal Housing Finance Agency, Case Shiller, or another source. Even more subtly, which data set within the FHFA data should a financial institution use – all transactions, purchase only transactions, seasonally or non-seasonally adjusted, etc. We use the seasonally adjusted, purchase-only HPI.
Identifying sources for future macroeconomic conditions can be even more challenging and we believe this could be the most challenging aspect of implementation because the standard requires “reasonable and supportable” forecasts. Continuing our residential real estate loan example, we use Case Shiller forecasts for the near term and revert to the Zillow national forecast over the long term.
Advantages of Using Discounted Cash Flow Models
Wilary Winn believes the discounted cash flow model approach to CECL estimates provides numerous advantages over the alternative loss measures such as vintage analysis or average charge-off method. More specifically:
- DCF models are widely used across the financial services industry and the Securities Industry and Financial Markets Association (“SIFMA”) has standardized the mathematical calculations. As a result, users do not have to come to agreement on the financial mathematics – e.g., how to calculate single month mortality – they can focus on how the model input assumptions were derived.
- DCF models explicitly include a methodology to account for voluntary prepayments, which must be considered as part of a CECL calculation.
- DCF models are prospective in nature and changes in expected macroeconomic conditions can be relatively easily incorporated into them. Wilary Winn begins with future expected contractual cash flows and modifies our model input assumptions based on macroeconomic forecasts. For example, Wilary Winn’s default rate assumptions for consumer and residential real estate loans are based on the existing and forecasted unemployment rate and we can easily incorporate expected changes in the unemployment rate into our models. Similarly, our loss severity assumption for residential real estate loans is based on the combined loan-to-value ratio of the loan. Our DCF models dynamically vector the combined LTV based on expected changes in housing prices. We believe this is much more straightforward and, thus more easily verified, than making environmental and qualitative adjustments to say a vintage analysis.
- We believe that because very few financial institutions will have a statistically valid sample of loan defaults at the cohort level, incorporating industry default data will be of critical importance to accurately forecast lifetime credit losses. Wilary Winn believes that the credibility theory approach in which industry performance data is included with a financial institution’s own loss experience (described previously in this white paper) is most easily accomplished with the discounted cash flow method by modifying the primary input assumptions CRR, CDR and loss severity.
- Wilary Winn believes that by segmenting the loan portfolio into predictive credit cohorts and then using FICO, combined loan-to-value ratios and credit risk rating to derive default assumptions can lead to better communication across the organization. For example, we believe it is much simpler to discuss FICO and combined LTV attributes for a used indirect vehicle loan portfolio with a financial institution’s lenders than it is to share the results of a vintage analysis adjusted for environmental and qualitative factors because FICO and LTV are key inputs that the lenders use to make credit decisions. The finance department is essentially speaking their language rather than discussing a high-level retrospective analysis that has been adjusted top down to derive prospective forecasts.
- We believe that dynamic, prospective DCF models based on the credit attributes an institution’s lenders use to make loans can lead to better allocations of capital. See our white papers Making the Business Case for CECL Part I – which addresses capital stress testing and Making the Business Case for CECL – Part II – which addresses concentration risk management. Finally, look for our Part III segment which will focus on lifetime credit losses and loan pricing – real return analysis.
Conclusion
Wilary Winn believes that the information financial institutions should collect as they work to implement CECL is primarily dependent on:
- The type of loans being assessed
- The credit risk model the financial institution plans to use
We also believe these factors are interdependent as we have shown in this white paper. We further believe that while the CECL standard permits the use of numerous methodologies for determining lifetime credit loss exposure, the use of dynamic, prospective discounted cash flow models offer multiple advantages over other methods, including better communication across the financial institution, more effective deployment of an organization’s capital, and increased accuracy in forecasting losses based upon assumed economic conditions. Appendix A provides a complete list of loan data elements needed to be collected in order to derive DCF precise model inputs to be used in projecting lifetime expected credit losses.
For full Appendix, please see PDF
Source
[1] FAS ASC 326-20-55-5